信號還原

抽樣之後的信號，其頻譜會不斷重覆，如果抽樣夠快，使用一個低通濾波器便可以把信號還原回來。在頻率乘上一個低通濾波器，等於在時域上和 sinc 函數做摺積，其還原信號公式如下:

$$x(t) = \sum_{n=-\infty}^{\infty} x(nT) \operatorname{sinc}(\frac{t-nT}{T})$$

現在試著使用以下程式碼做信號的還原：

srate = 2;         % 抽樣速度
st = (-8:8)/srate; % 抽樣點
xn = mys(st);      % 信號值

N = floor(length(xn)/2);  % 點數一半
t = -5:0.1:5;             % 計算還原信號的時間點
rt = zeros(size(t));
for n=-N:N
  rt = rt + xn(n+N+1)*sinc((t-n/srate)*srate);
end
plot(t,rt), grid on;
xlabel('t'), ylabel('s(t)');
title('Reconstructed Signal');

得到的圖形如下。

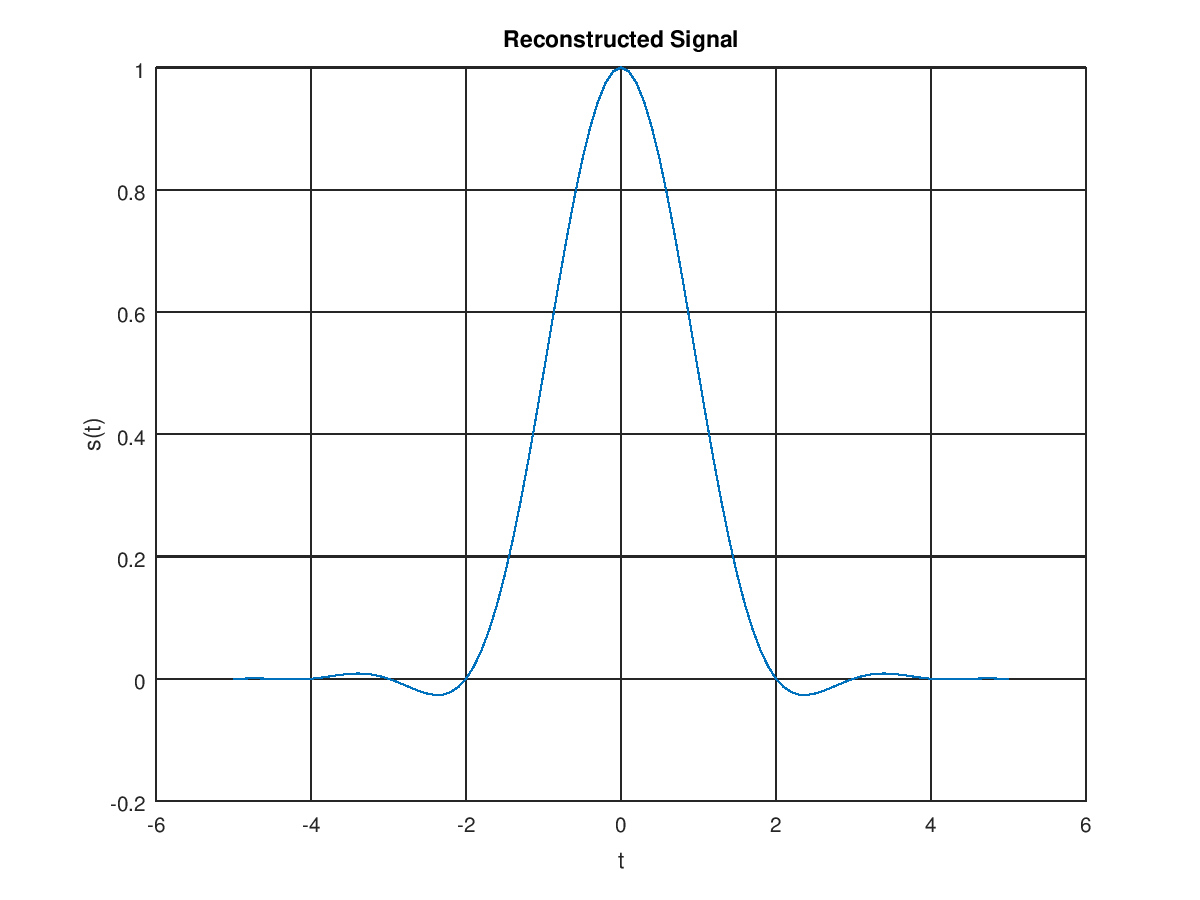還原的升餘弦脈衝信號, fs=2

練習

試著調整不同的抽樣速度，例如大於或小於信號最高頻率的兩倍，計算還原的信號與原來信號的誤差。