抽樣頻譜

抽樣之後，頻譜會變成重覆的狀況，為了方便，我們再寫一個計算重覆頻譜的函數，取名為 myssf.m，程式碼如下：

function y = myssf(x, fs)
% Calculate repeated sampled spectrum of raise cos

y = zeros(size(x));
for k=-5:5
y = y + mysf(x-k*fs);
end

取 fs=1，試用一下所寫的函數：

f = -2:0.1:2;
sf = myssf(f, 1);
plot(f, sf);
grid on;

得到的圖形如下圖所示：

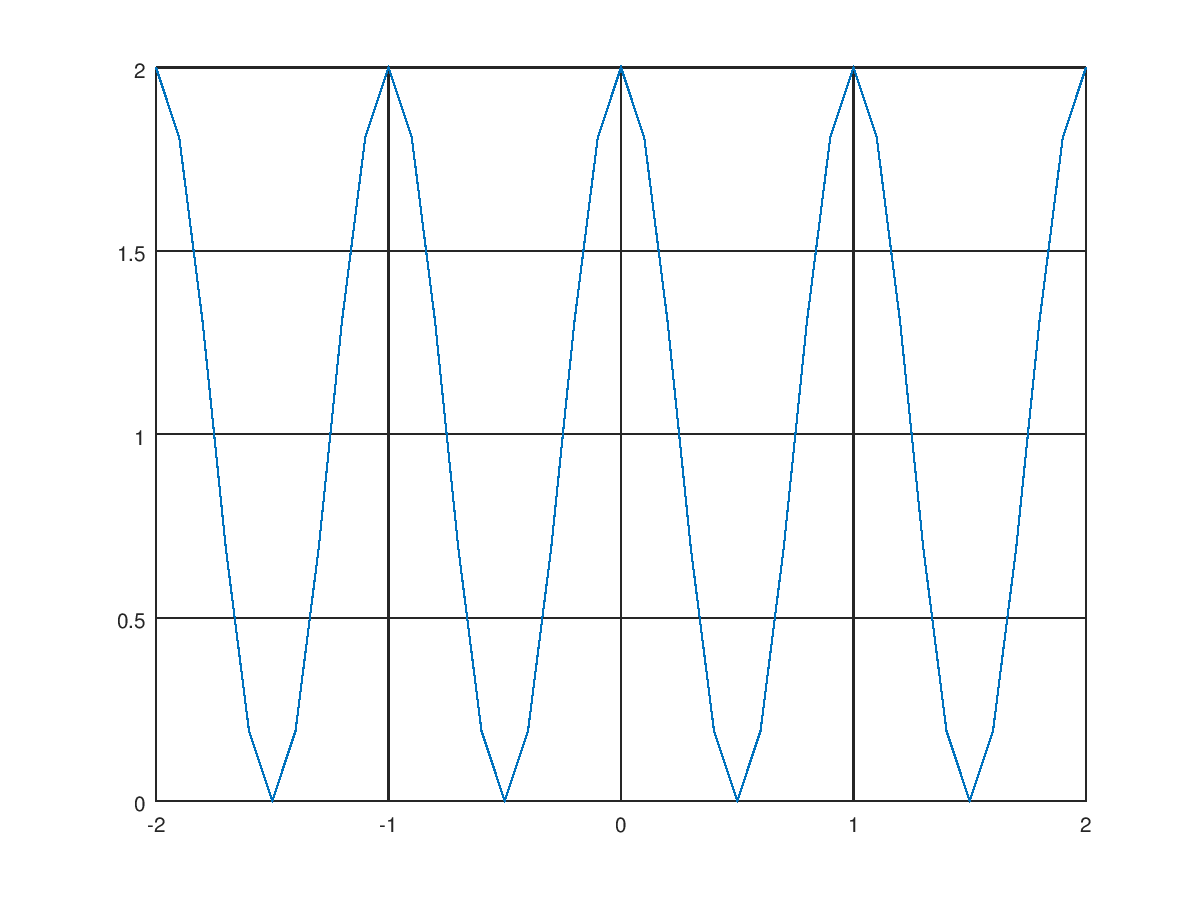升餘弦脈衝信號抽樣後的頻譜, fs=1

現在回來做數值計算。對於一個函數 $x(t)$ 抽樣，可以看成把 $x(t)$ 乘上 $\delta(t)$ 函數的陣列，如下式所示：

$$x_{\operatorname{sample}}(t) = \sum_{n=-\infty}^{\infty} x[nT]\cdot\delta(t-nT)$$

其傅立葉轉換為

$$X(f) = \sum_{n=-\infty}^{\infty} x_n\cdot e^{-i2\pi fnT}$$

一般我們會使用數位傅立葉變換 (DFT) 來計算 $X(f)$ 的抽樣值，其公式如下:

$$X_k = \sum_{n=0}^{N-1} x_n\cdot e^{-i\frac{2\pi}{N}kn}$$

$X_k$ 可以看成頻率正規化後在角頻率 $kn/N$ 的大小。我們可以使用以下的程式來計算抽樣之後的頻譜。

Ts = 1;        % 抽樣間隔
t2 = -4:Ts:4;  % 抽樣時間點
fst = mys(t2); % 抽樣值 xn
N = 8;         % 角頻率半週點數 (pi)
r = 4;         % 角頻率重覆週數
k = -N*r:N*r;  % 角頻率點數範圍
w = pi*k/N;    % 角頻率向量
Fsw = Ts*fst*exp(-j*t2'*w); % 角頻率分量計算公式
plot(w, abs(Fsw), 'o-');
axis([-4*pi 4*pi -0.2 2.1]);
xlabel('\omega'), ylabel('Fs(\omega)');
title('Spectrum of Sampled Raised Cosine');

其結果如下圖所示：

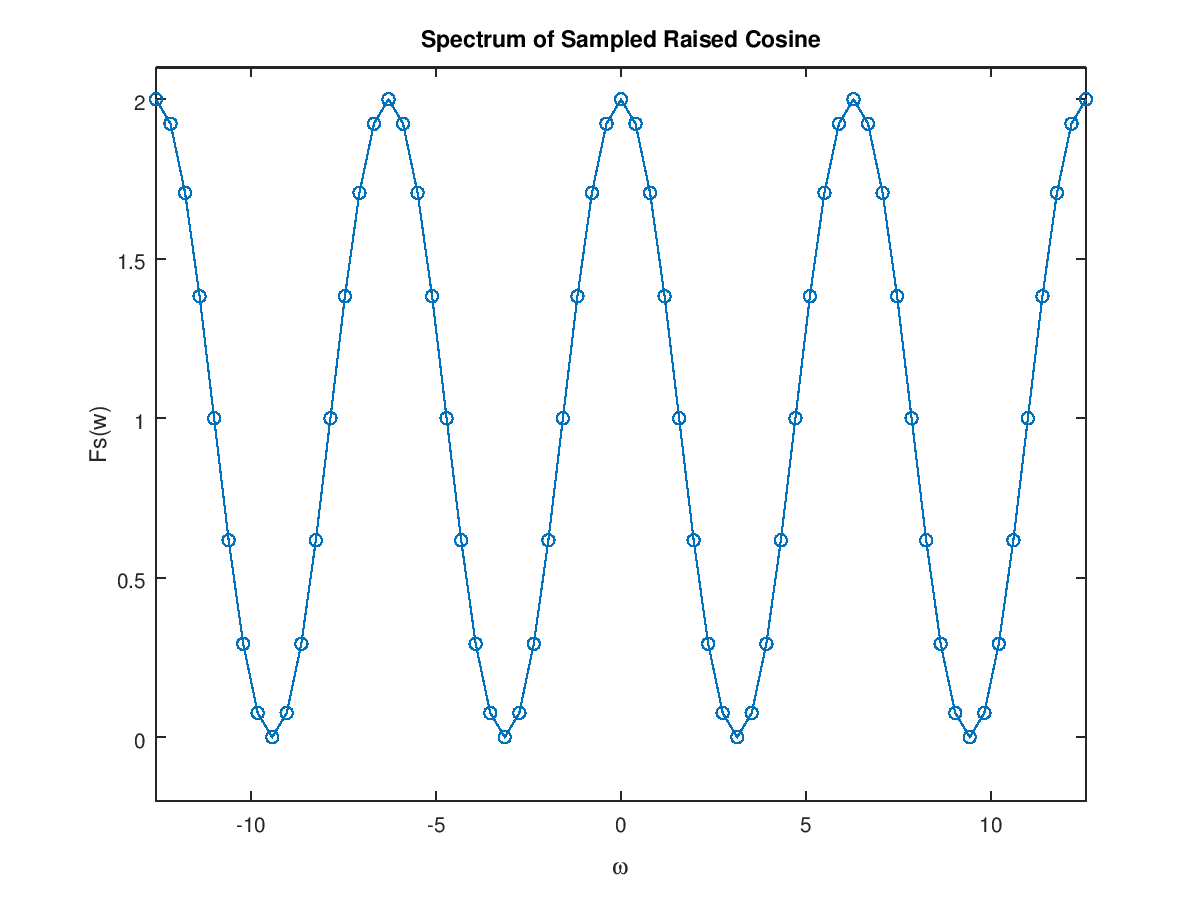升餘弦脈衝信號取樣後的頻譜, fs=1

這個結果和我們用 myssf 計算出來的是一樣的,唯一的差別是橫軸放大了 $2\pi$，有興趣的同學可以驗證一下。