傅立葉級數

函數有不同頻率成份，可以看成是由不同頻率成份的函數組合而成，而傅立葉分析主要就是用來觀察和分析函數的各種不同頻率成份。

一般周期性信號的頻率成份，會有一個最低的頻率成份稱為基頻，其他頻率成份會是這個頻率的倍數，也可以說是相關的諧波。這些頻率成份的系數，可以使用傅立葉級數來計算。如果信號不是周期性的，但是有一個限制的區間，那我們也可以把這個區間重複延伸，看成是周期性的函數。

假設函數 $s(x)$ 定義在 $[x_0, x_0+P]$ 的區間，則其傅立葉級數為

$$\frac{a_0}{2} + \sum_{n=1}^{\infty} (a_n\cos(\frac{2\pi n x}{P}) + b_n\sin(\frac{2\pi n x}{P})),$$

其中

$$a_n = \frac{2}{P}\int_{x_0}^{x_0+P} s(x)\cos(\frac{2\pi n x}{P})\ dx$$

$$b_n = \frac{2}{P}\int_{x_0}^{x_0+P} s(x)\sin(\frac{2\pi n x}{P})\ dx$$

$a_n$ 及 $b_n$ 為 $n$ 階諧波的系數。

接下來，我們要使用 MATLAB 來觀察一個鋸齒狀的三角波，我們把它的傅立葉級數的係數算出來，然後把 $N$ 項諧波的成份加起來，和原來波形放在一起觀察。 這邊使用的波形 $s(t)$ 函數如下：

可以算出其傅立葉級數為：

$$s(t) = \frac{2}{\pi}\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}\sin(nx)$$

MATLAB 程式步驟如下：

1. MATLAB 有一個 sawtooth 函數，可以直接畫出鋸齒波形。sawtooth 定義在 Signal Processing 工具箱，如果使用 MATLAB，必須確定此工具箱已正確安裝；如果使用 Octave，則可以使用 signal 套件。關於 Octave 套件的安裝方式，在 Windows 環境下，可參考 官網的說明 (opens new window)，如果是在 Ubuntu 的話，直接使用以下指令進行安裝：

sudo apt-get install octave-signal

2. 在 Octave 裡面，先使用 pkg load signal 指令將 Signal Processing 套件載入。接著便可以使用 sawtooth 函數（可用 help sawtooth 查看此函數的使用說明）。試著使用以下指令畫出 sawtooth 函數圖形：

t = -8:0.1:8;
s = sawtooth(t-pi); % sawtooth 預設周期為 2*pi，在 0 的地方轉折
plot(t,s);
grid on; % 畫格線		

觀察一下波形看是否正確。

3. 畫部分級數和。

N = 5;   % 項數
sgn = 1; % 用作正負變號使用，第一項為正
t = -8:0.1:8; 
fs = zeros(size(t)); % 設 fs 跟 t 維度一樣，全為 0
for n = 1:N          % 從 1 跑到 N
	fs = fs + 2*sgn*sin(n*t)/(n*pi); % 加一項
	sgn = sgn * -1;  % 變號
end
plot(t,fs); % 畫圖

觀察一下合成的波形。

4. 最後將兩個波形畫在一起，程式碼如下：

N = 5;
t = -8:0.1:8;
sgn = 1;
s = sawtooth(t-pi); % sawtooth 預設周期為 2 pi，在 0 的地方轉折
fs = zeros(size(s));
for n = 1:N
    fs = fs + 2*sgn*sin(n*t)/(n*pi);
    sgn = sgn * -1;
end
plot(t,s,'b',t,fs,'r');
grid on; % 畫格線

執行後的結果如下：

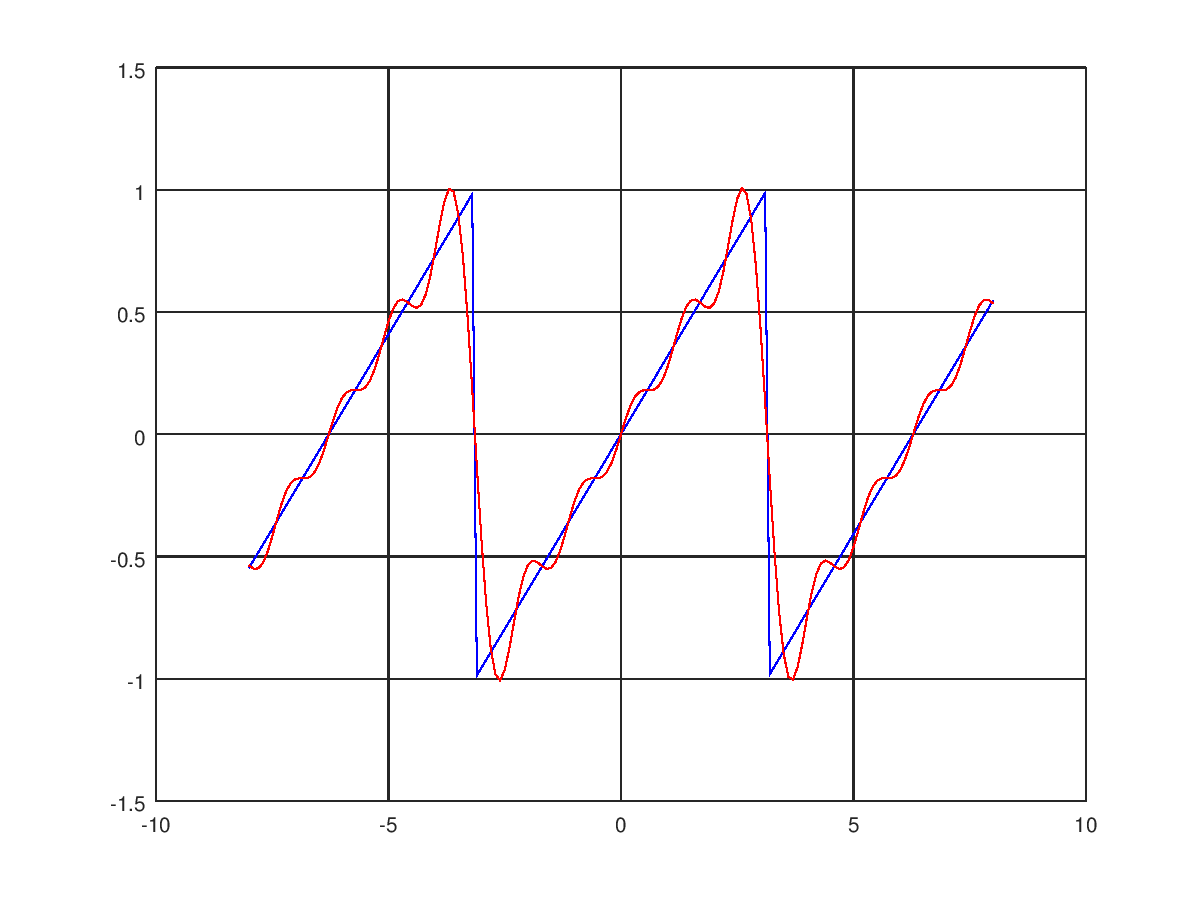
在上面的程式中，我們已經知道 $s(t)$ 的傅立葉級數的 $a_n$ 和 $b_n$ 的系數，如果是其他函數的話，可能要花很多時間計算。實際上，MATLAB 有一個 Symbolic Math Toolbox，可以幫忙做符號運算。

如果是使用 Octave，可以先用以下指令安裝 symbolic 套件：

sudo apt-get install octave-symbolic

接著用 pkg load symbolic 載入套件來使用。

例如 $f(x)=x^2$，假設定義在 $[-\pi,\pi]$ 的區間，可以使用以下方式計算 $a_n$ 的係數。

pkg load symbolic
syms x n;    % x, n 為符號
f = x^2;     % f(x) = x^2
an = int(f*cos(n*x), x, -pi, pi) / pi;    % 計算定積分的值

練習 3

MATLAB 裡面有一個 square 函數，可以用來畫出方波函數 (用 help square 查詢看看)。請利用 symbolic 套件來計算方波的傅立葉級數，接著用程式畫出方波及其部分傅立葉級數和的圖形，此處方波的周期和振幅可自己定義。