抽樣定理

抽樣定理是將類比信號轉換成數位信號很重要的一個關鍵。假設信號為 $x(t)$，其傅立葉變換為 $X(f)$，則

$$X(f) = \int_{-\infty}^{\infty}x(t)\ e^{-j2\pi ft}\ dt$$

一般我們把抽樣過程看成是原來時域函數乘上一個 $\delta$ 函數陣列，假設時間軸每隔 $T$ 取一點，其抽樣值為 $x(nT)$，且 $X_s(f)$ 為 $x(t)$ 抽樣後的頻譜，則

$$X_s(f) = \sum_{k=-\infty}^{\infty}X(f-kf_s)$$

其中 $f_s$ 為抽樣速度。示意圖如下：

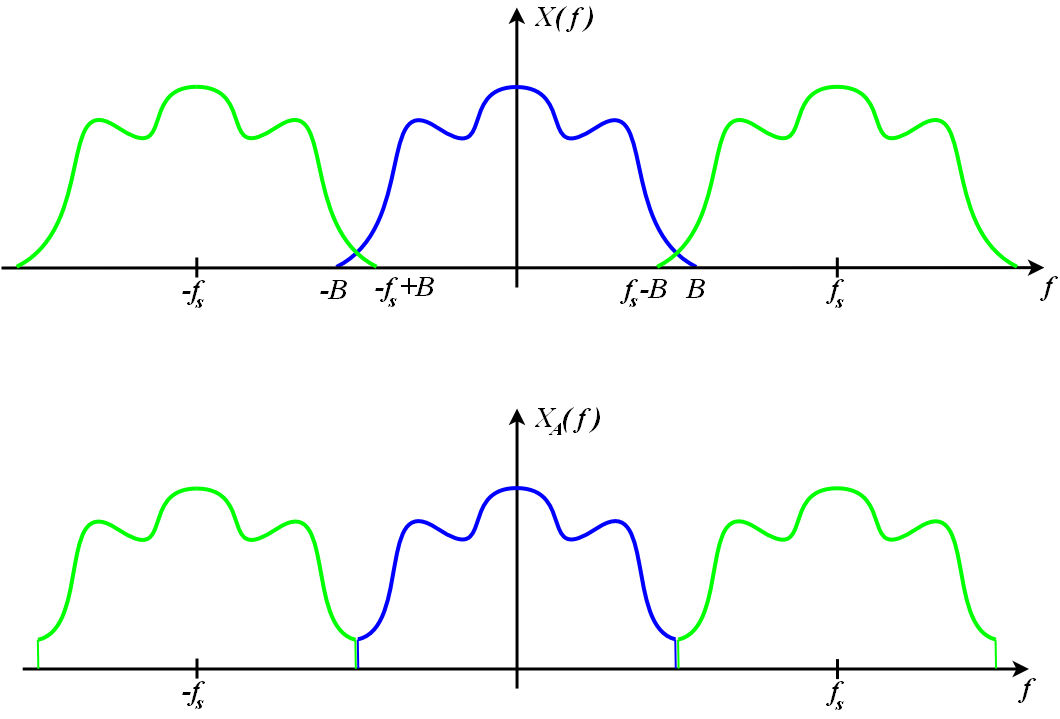抽樣之後的頻譜

註意在上圖中，原來的頻譜每隔 $f_s$ 會重覆一次，直觀來看，也就是抽樣後，頻率 $f$ 和頻率 $kf_s+f$ 根本無法區分，可以看成是一樣的。如果 $f_s>2B$，也就是抽樣速度超過最大頻率的兩倍，那麽重覆的頻譜之間不會重疊；反之，則會重疊並產生干擾，如上圖所示。

抽樣定理告訴我們，只要抽樣速度超過最大頻率兩倍，那麽重覆的頻譜不會重疊，我們就可以使用一個低通濾波器把原來的信號頻譜找回來，如下圖所示：

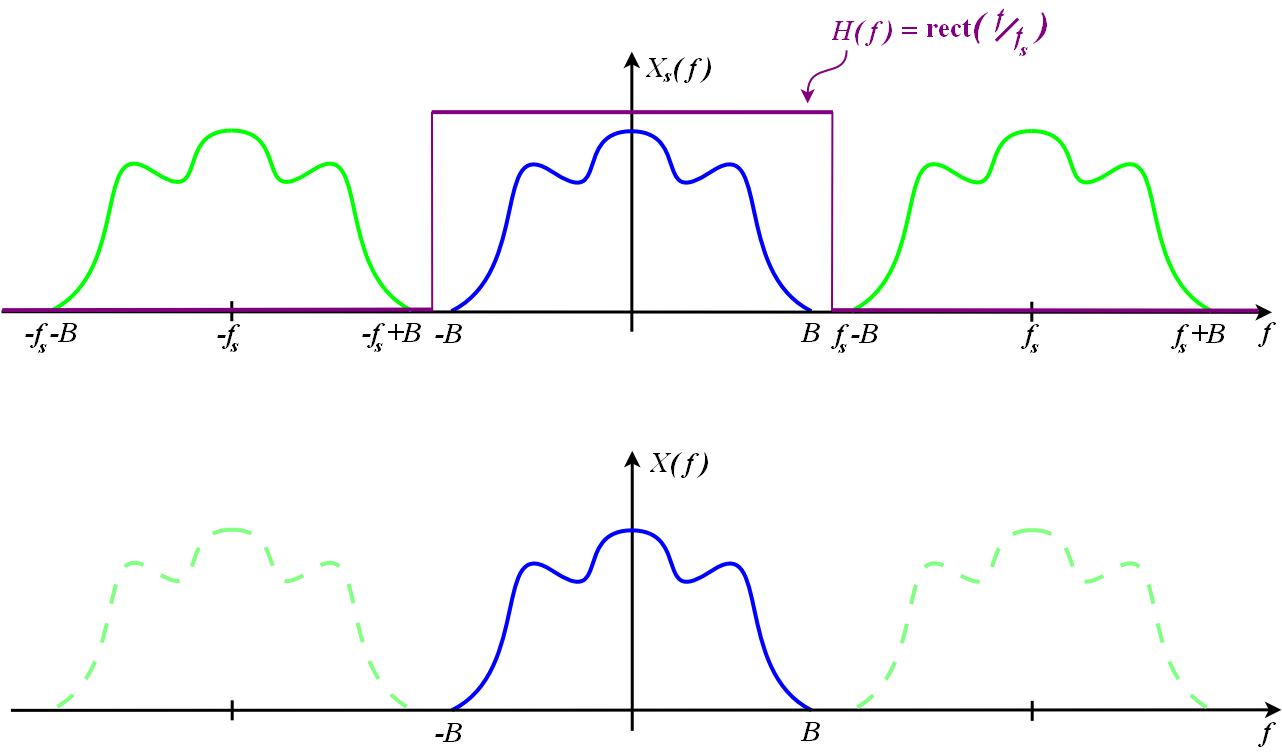
使用低通濾波器取回原來的頻譜

為了進一步了解抽樣定理，以下我們將使用 MATLAB/Octave 程式來進行模擬。