基本语法

这边只针对实验内容会用到的基本程式语法做简单介绍，如果想更深入了解，可以自行借阅 MATLAB 相关的书籍研习。

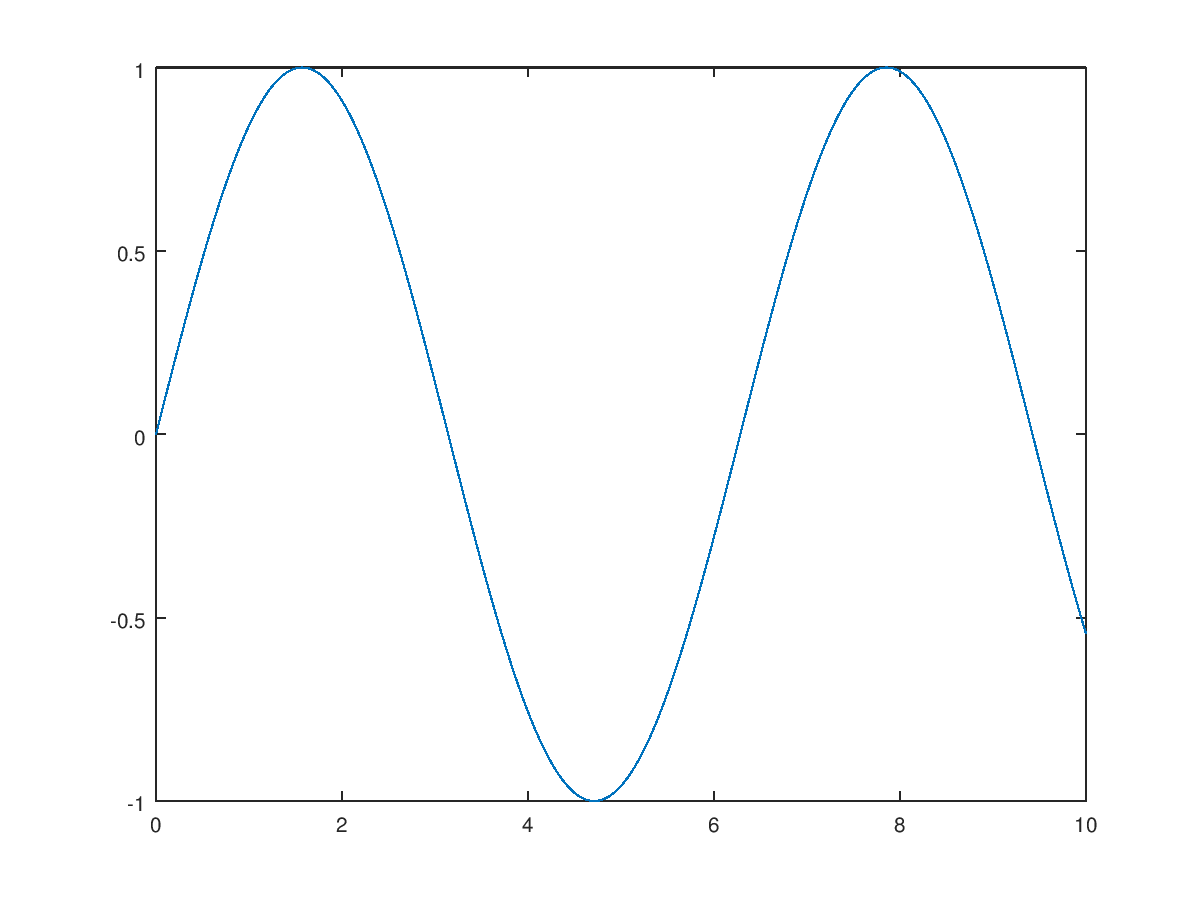
1. 画出 sin(t) 函数图形

% 百分比符号后面代表注解，式子后面不加分号的话，会显示计算结果
t=0:0.01:10;   % 产生一维矩阵,从 0 开始,间隔为 0.01,到 10 为止
x=sin(t);      % 计算 t 的 sin 函数值(各元素计算)，结果仍为一维矩阵
plot(t,x);     % t 为横坐标，x 为纵坐标，画图 t=0:0.01:10;

结果如下图：

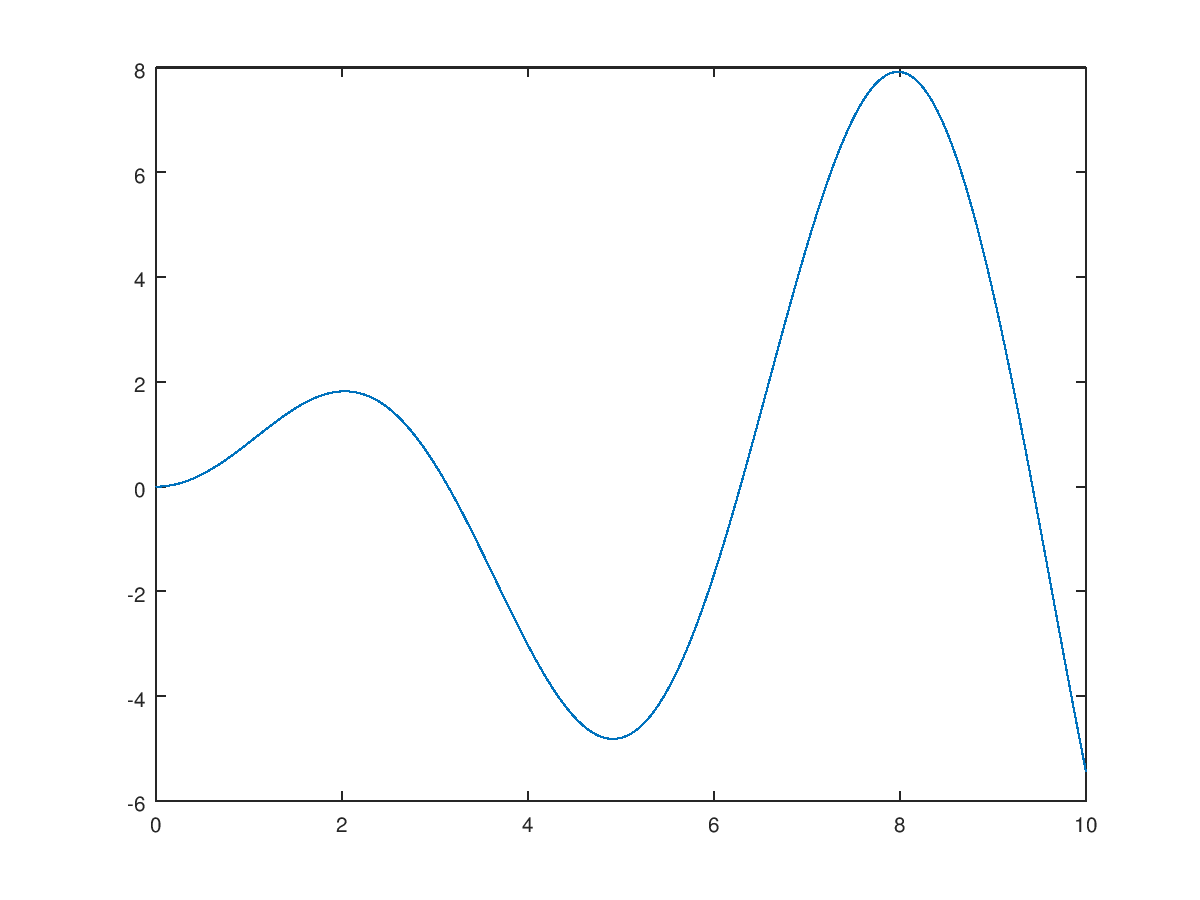
2. 画出 t*sin(t) 函数图形
   基本上MATLAB把每个变数视为矩阵，可以计算加减乘除，但都是以矩阵形式做运算，如果希望计算的是矩阵和矩阵内对应元素的加减乘除的话，可以在加减乘除的运算符号前加上一个小数点。

t=0:0.01:10;  % 产生一维矩阵，从 0 开始，间隔为 0.01，到10为止
x=t.*sin(t);  % 以元素方式计算 t 乘上 sin 的函数值
plot(t,x);    % t 为横坐标，x 为纵坐标，画图

结果如下图：

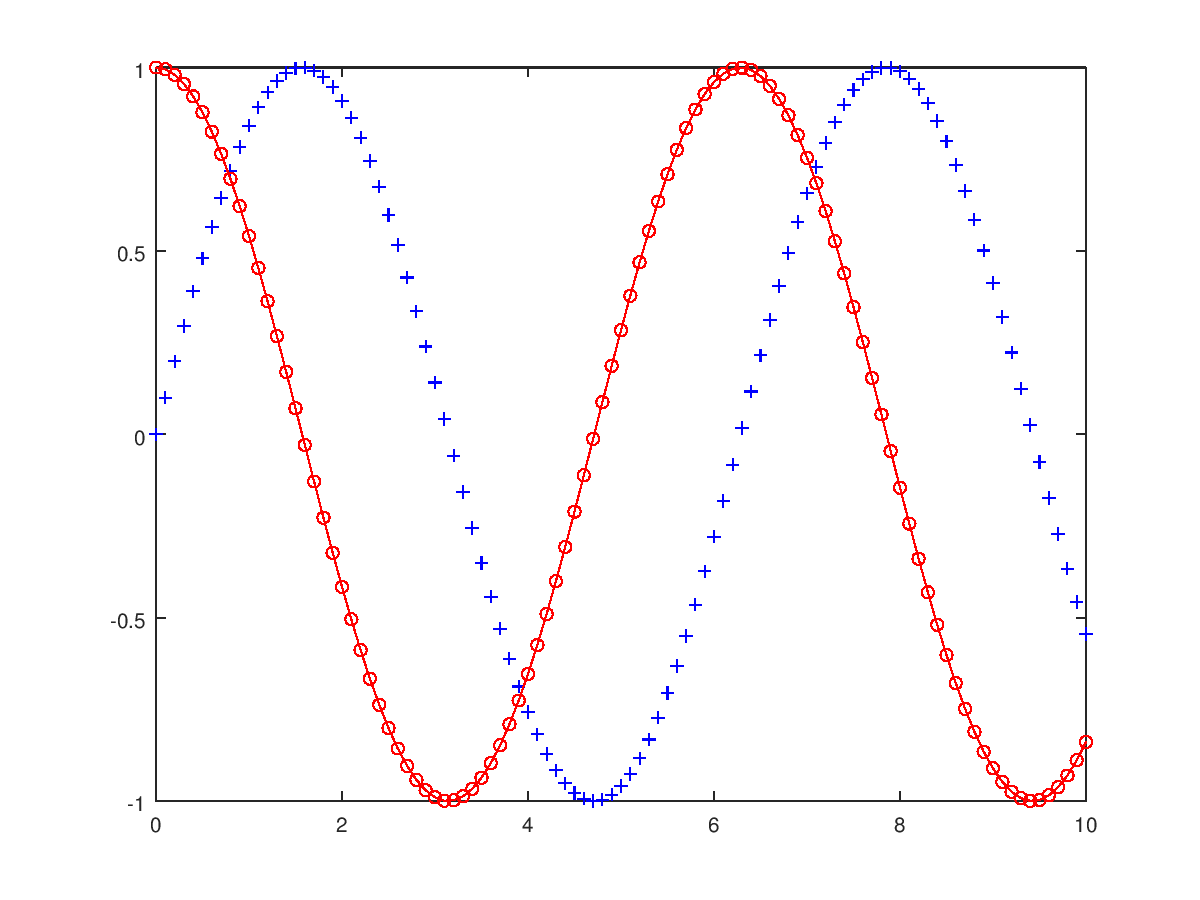
3. 画多个图形
   将 sin(t) 和 cos(t) 的图形画在一起，并加上简单的样式：

t=0:0.1:10;
x1=sin(t);
x2=cos(t);
plot(t,x1,'+b',t,x2,'o-r');     % b：蓝色，r：红色，-：连线，+o：点

结果如下图：

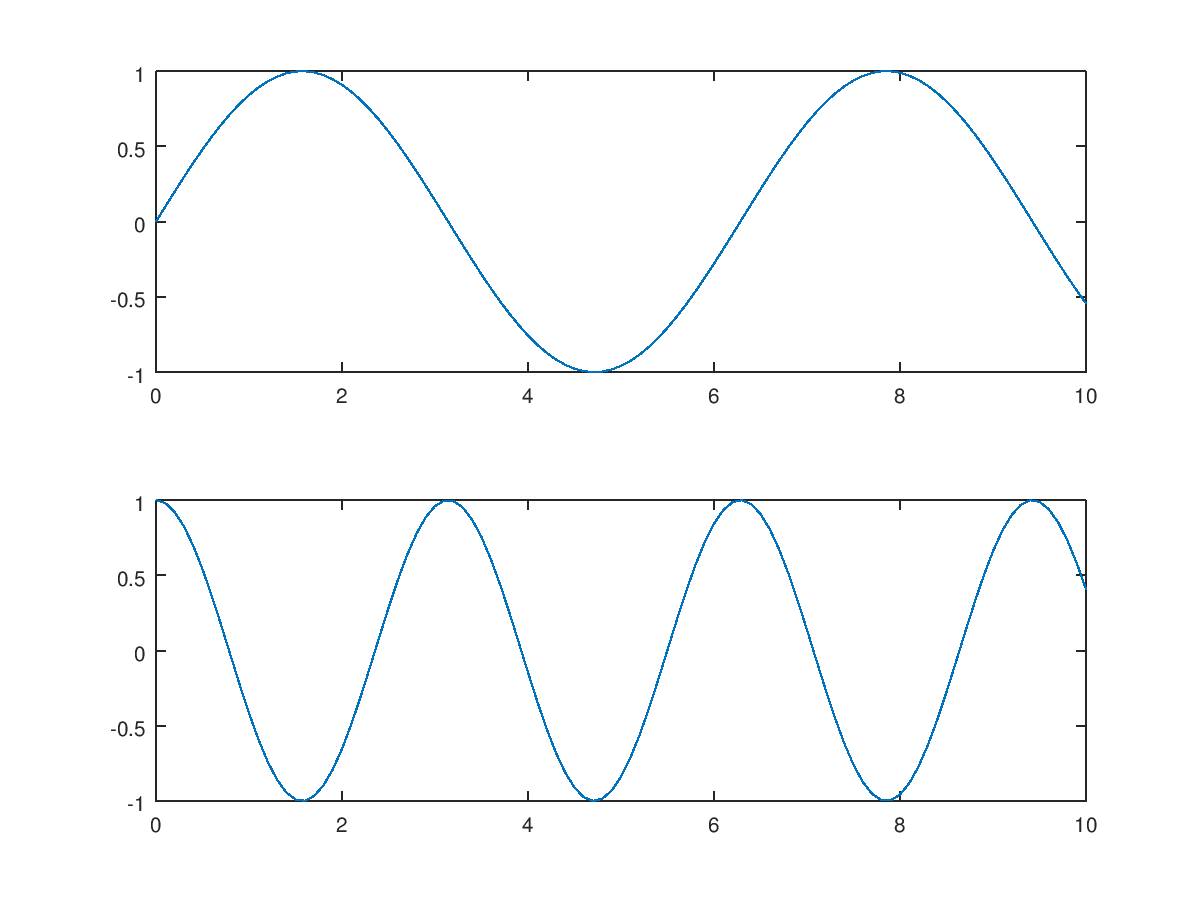
4. 分割画图
   画出 sin(t) 和 cos(2t) 的图形，sin(t) 在上面，cos(2t) 在下面：

t=0:0.1:10;
x=sin(t);
y=cos(2*t);
subplot(211); plot(t,x);   % 2 列 1 行, 第一个图
subplot(212); plot(t,y);   % 2 列 1 行, 第二个图

结果如下图：

練習 2

画出三个图形，排成上中下，依次为 $\cos(100\pi t)$, $\cos(1000\pi t)$ 以及 $\cos(100\pi t)\cos(1000\pi t)$ (注：$\pi$ 可直接用 pi 表示)。