傅立叶转换

非周期性函数的频率成份是连续的，我们可使用傅立叶转换来计算其频率密度函数，假设时域函数为 $s(t)$，其傅立叶转换公式如下：

$S(f) = \int_{-\infty}^{\infty}f(x)\ e^{-j2\pi ft}\ dt$

一般在信号处理时，我们多使用快速傅立叶转换 (FFT) 来计算其频谱，使用快速傅立叶转换时，应牢记以下几个重点：

1. 假设用来分析的信号段有 $N$ 个点，且其取样间隔为 $\Delta t$，则此信号段总长为 $T=N\Delta t$，且取样速度为 $R=1/\Delta t$。

2. 根据取样定理，可以观察的频率范围为 $[-f_0,f_0]$，$f_0=R/2$。

3. $N$ 个时域点做 FFT 之后变成 $N$ 个频域点，故频率解析度，亦即相邻频率点的间隔为 $2f_0/N = R/N = 1/(N\Delta t) = 1/T$。
   简单说，取样时间总长的倒数就是频率取样点之间的距离，也就是频率解析度。

4. 要记得取样速度的一半，是可观察的最大频率；取样总长的倒数是频率解析度。

5. 如果是实函数的话，做完 FFT 之后，其正频率和负频率相对的值会是共轭复数。

我们现在来观察帽子函数的频谱，定义帽子函数 rect(t) 如下：

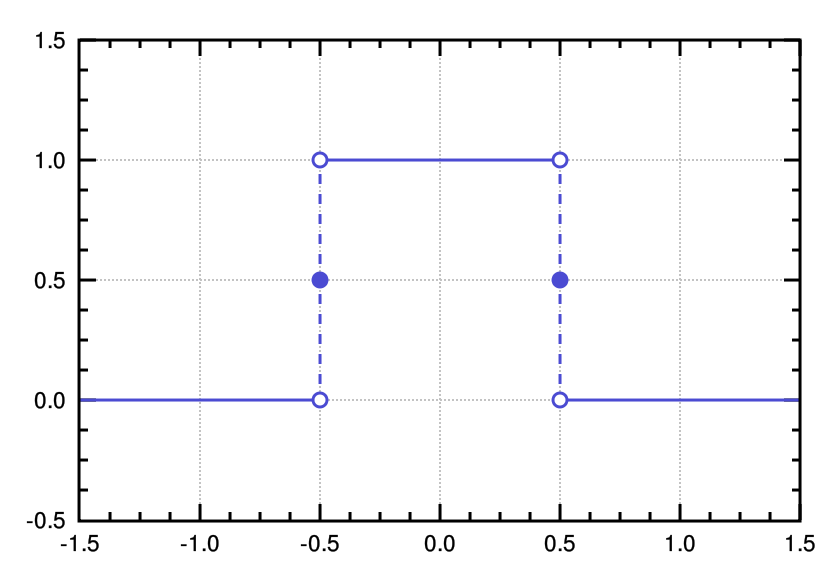
使用 MATLAB 观察其频谱步骤如下：

1. 假设取样范围从-1.5到1.5，每隔0.1取一点，先计算时域信号：

t1 = -1.5:0.1:-0.6;
t2 = -0.4:0.1:0.4;
t3 =  0.6:0.1:1.5;
t = [t1 -0.5 t2 0.5 t3];
s = [zeros(size(t1)) 0.5 ones(size(t2)) 0.5 zeros(size(t3))];
plot(t, s);

这个程式片段写得有点繁琐，不过很容易理解，看一下结果是否正确。

2. 计算频谱，直接使用 fft 函数将上面的时域信号转到频域，应注意转出来的结果为复数，我们先观察其振幅。

sf = fft(s);
plot(abs(sf));

注意在上面的程式中，画图时只给了y轴，横轴会是点数，得到的结果如下：

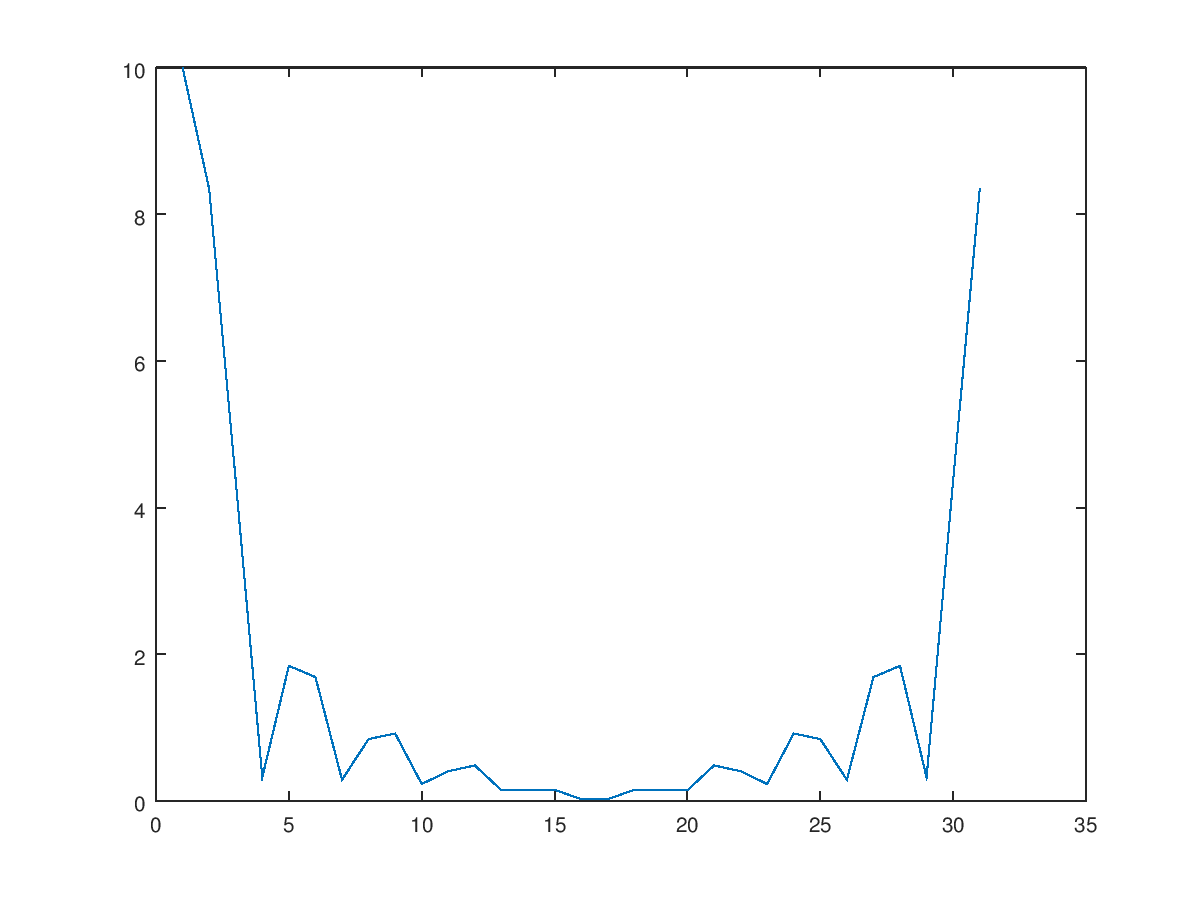
3. 上面提过实函数的 FFT，其正频率和负频率相对的值是共轭复数。实际上我们现在看到的图形中，图的右半边应该移到负的那边去才对。MATLAB 里面有一个 fftshift 就做这事。另外，最大频率为取样率一半=5，间隔为总长倒数=1/3，我们要把横轴 (频率) 加上去。

sf = fft(s);
sf = abs(fftshift(sf));
f = -5:1/3:5;
plot(f, sf);
grid on;

最后得到修正的图如下，这个图形就是 sinc 函数的振幅。

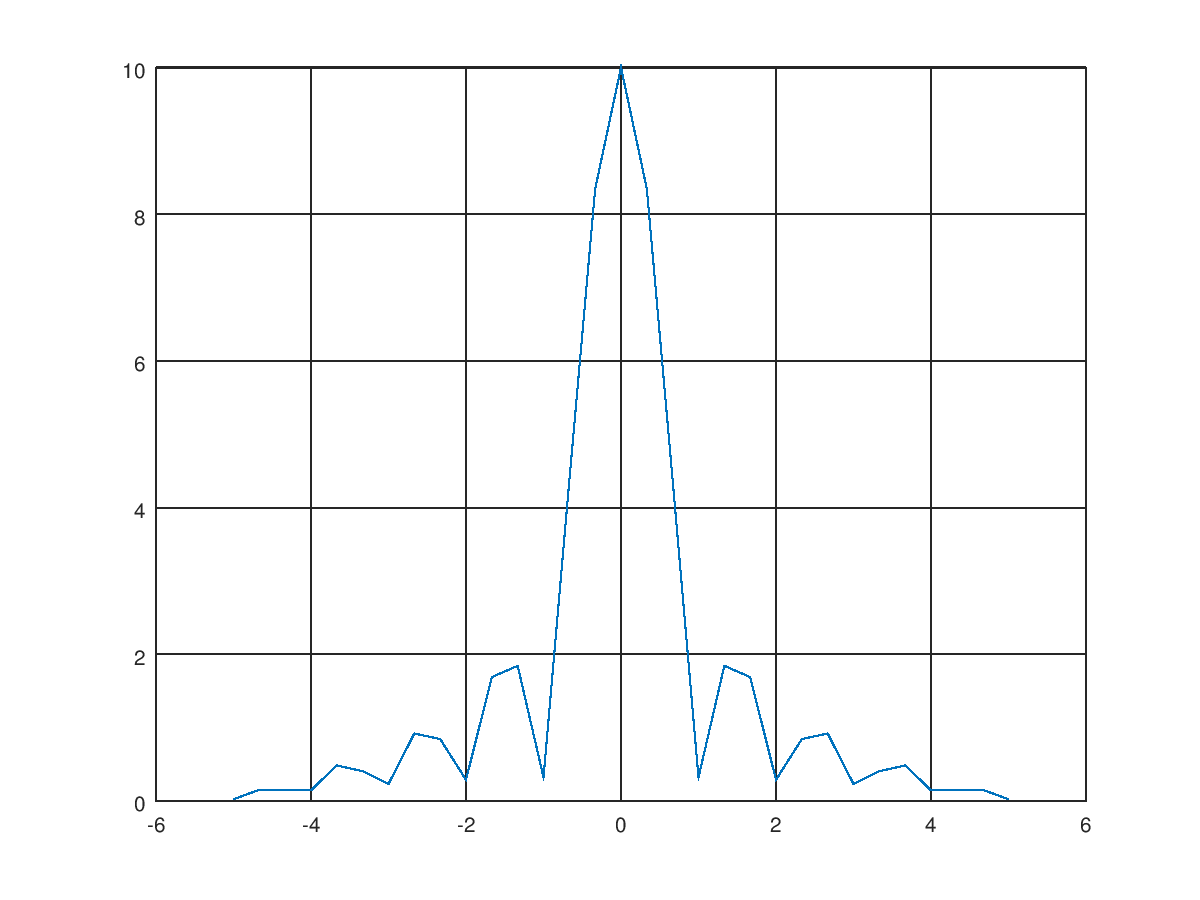
完整程式码如下：

t1 = -1.5:0.1:-0.6;
t2 = -0.4:0.1:0.4;
t3 =  0.6:0.1:1.5;
t = [t1 -0.5 t2 0.5 t3];
s = [zeros(size(t1)) 0.5 ones(size(t2)) 0.5 zeros(size(t3))];
sf = fft(s);
sf = abs(fftshift(sf));
f = -5:1/3:5;
plot(f, sf);
grid on;

練習 4

请分析时域函数 rect$((t-1)/2)\cdot\cos(20\pi t)$ 的频谱。